Conalep
Analisis integral de las funciones
Integrantes: Kennya Maya Sanchez.
Rogelio Garfias Benteño.
Dario Victoria Martinez
Nancy Karina Perez Salgado.Dario Victoria Martinez
Juan Carlos Rojas Arenazas.
Luis Arnulfo Garduño Gonzalez.
Maestra: Edith Suarez Garcia.

Integral indefinida
Integral indefinida es el
conjunto de las infinitas
primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x
diferencial de x.
∫ es el signo de
integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la
variable de la función que se integra.
C es la constante de integración y puede
tomar cualquier valor numérico real.
Si F(x) es una primitiva de
f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de
una función es correcta basta con derivar.
Propiedades
de la integral indefinida
1. La integral de una suma de funciones
es igual a la suma de las
integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por
una función es igual a la constante
por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx
Las formulas de las integrales son:
Las formulas de las integrales son:

Determinación
de diferenciales.
Interpretación
grafica de la diferencial de la variable dependiente.
Una
variable dependiente es aquella cuyos valores dependen de los que tomen otra
variable.
La
variable dependiente en una función se suele representar por y.
La
variable dependiente se representa en el eje ordenadas.
La
variable y está en función de la variable x, que es la variable independiente.
Ejemplos
El
precio que pagamos por las patatas depende del número de kilogramos que
compremos.
x
= Kg de patatas 1 2 3 4 5
y
= Precio en € 2 4 6 8 10
El
precio de un viaje en taxi viene dado por:
y
= 3 + 0.5 x
Siendo
x el tiempo en minutos que dura el viaje.
x
10 20 30
y=
3 + 0.5x 8 13 18
Reglas
de diferenciación.
Función
de una variable-de forma
!
Y
= f (x) donde f significa cualquier función. En
Economía,
generalmente, suponemos que las funciones son continuamente
Diferenciables.
k es un constante.
1.
Regla de la función constante
Determinación
de diferenciales.
Interpretación
grafica de la diferencial de la variable dependiente.
Una
variable dependiente es aquella cuyos valores dependen de los que tomen otra
variable.
La
variable dependiente en una función se suele representar por y.
La
variable dependiente se representa en el eje ordenadas.
La
variable y está en función de la variable x, que es la variable independiente.
Ejemplos
El
precio que pagamos por las patatas depende del número de kilogramos que
compremos.
x
= Kg de patatas 1 2 3 4 5
y
= Precio en € 2 4 6 8 10
El
precio de un viaje en taxi viene dado por:
y
= 3 + 0.5 x
Siendo
x el tiempo en minutos que dura el viaje.
x
10 20 30
y=
3 + 0.5x 8 13 18
Reglas
de diferenciación.
Función
de una variable-de forma
!
Y
= f (x) donde f significa cualquier función. En
Economía,
generalmente, suponemos que las funciones son continuamente
Diferenciables. que es un constante.
A continuación mostraremos como realizar una integral de una forma detallada...
Las cuales utilizamos para elaborar estos ejercicios:
2 NOTACIÓN SUMATORIA
Notación sigma.
En la sección anterior hemos estudiado la
antiderivación. En esta sección investigaremos un problema referente al cálculo
del área de una región en el plano. A primera vista, parece que esos dos
conceptos no tengan relación alguna. No obstante, descubriremos que están
íntimamente ligados por el importantísimo teorema fundamental del Cálculo.
Empezamos introduciendo una notación concisa para las
sumas, que se denomina notación sigma debido a que utiliza
la letra griega Σ, la sigma mayúscula.
NOTACIÓN SIGMA.
La suma de n términos  se escribe
se escribe
donde i es el
índice de suma, ai es el i-ésimo término de la suma, y los límites
inferior y superior de la suma son 1 y n.
Nota: Los límites inferior y
superior de la suma han de ser constantes respecto del índice de suma. Sin
embargo, el límite inferior no tiene por que ser 1. Cualquier entero menor o
igual que el límite superior es lícito.
Las siguientes propiedades se deducen usando las
leyes asociativa y conmutativa de la suma y la distributiva de la suma respecto
de la multiplicación. (En la primera propiedad, k es una constante.)
1. 
2. 
Concepto de
integral definida en un intervalo
Dada una función f(x) y un intervalo [a,b],
la integral definida es igual al área limitada entre la
gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.

La integral definida se representa
por  .
.
∫ es el signo
de integración.
a límite
inferior de la integración.
b límite
superior de la integración.
f(x) es el integrando o
función a integrar.
dx es diferencial
de x, e indica cuál es la variable de la función que se integra.
Propiedades de la integral definida
1. El valor de la integral
definida cambia de signo si se permutan los límites de integración.
2. Si los límites que
integración coinciden, la integral definida vale cero.
3. Si c es un punto
interior del intervalo [a, b], la integral definida se descompone
como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
4. La integral
definida de una suma de funciones es igual a la suma de integrales·
5. La integral del
producto de una constante por una función es igual a la constante por la
integral de la función.
Formulas directas
Sean a, b, e y k constantes (números reales)
y consideremos a: u(x) y v(x) como funciones.
En adelante, escribiremos u y v con el fin de
simplificar.
Derivada de una constante
Derivada
de x
Derivada
de la función lineal
Derivada
de una potencia
Derivada
de una raíz cuadrada
Derivada
de una raíz

Derivada
de una suma
Derivada
de una constante por una función
Derivada
de un producto
Derivada
de una constante partida por una función
Derivada
de un cociente
Derivada
de la función exponencial
Derivada
de la función exponencial de base e
Derivada
de un logaritmo
Como  ,
también se puede expresar así:
,
también se puede expresar así:
Derivada
del logaritmo neperiano
Derivada
del seno
Derivada
del coseno
Derivada
de la tangente
Derivada
de la cotangente
Derivada
de la secante
Derivada
de la cosecante
Derivada
del arcoseno

Derivada
del arcocoseno

Derivada
del arcotangente
Derivada
del arcocotangente
Derivada
del arcosecante

Derivada
del arcocosecante

Derivada
de la función potencial-exponencial
Regla
de la cadena
Derivadas
implícitas
PROBLEMAS DE ALGUN CONTEXTO
A continuación, mostramos cuatro de los problemas utilizados en
las cuatro últimas PL (6, 7, 8 y 9) en las que centraremos nuestro análisis.PROBLEMA 1
Dada la función f(x) = 3x4 - 4x3 - 12x2 + 5
a) Aproxima mediante los métodos gráfico y numérico el área bajo la curva en el intervalo [-1, 2.5].
b) Aproxima mediante los métodos gráfico y numérico el valor de la integral definida en el intervalo [—1, 2.5].
c) Calcula, utilizando el Teorema Fundamental del Cálculo, el área de la región en el intervalo [—1, 2.5].
d) Calcula, utilizando el Teorema Fundamental del Cálculo, la integral definida en el intervalo [—1, 2.5].
Este problema se enmarca en el contexto matemático. Se trata de una función continua para la que se pide el cálculo del área/integral por los distintos métodos que aparecen incluidos en el PU. La gráfica de la función posee partes situadas tanto por arriba del eje OX como por debajo de éste, lo que permite distinguir cuando se puede interpretar como un área la integral definida.
PROBLEMA 2
Dada la función

b) Si es posible, estima el valor de la integral definida en el intervalo [-2, 3]. Si no es posible, explica por qué.
Al igual que en el problema anterior, éste pertenece al contexto matemático. Se trata de una función continua a trozos para la que se pide el cálculo del área/integral en un cierto intervalo que contiene los puntos de discontinuidad.
PROBLEMA 3
Una partícula se mueve a lo largo de una recta, de modo que su velocidad es v(t) = t2 — 2t — 8, donde el tiempo es t. La velocidad se expresa en metros por segundo.
a) Calcula el desplazamiento de la partícula en el periodo 1 ≤ t ≤ 6.
b) Calcula la distancia recorrida durante este lapso (Stewart, 1999, p. 354, 357).
Éste es un problema en el contexto de la cinemática. Se involucran en él diversos conceptos de Física tales como velocidad, posición, distancia recorrida. La integral ayuda a identificar la relación que existe entre estos conceptos.
PROBLEMA 4
Una empresa de Ingeniería se ofrece a construir un túnel. Éste tiene 300 pies de largo por 50 pies de ancho. La forma del túnel es un arco cuya ecuación es y = 25 cos (πx/50). La parte superior del túnel se tratará con un sellador impermeable que tiene un costo de 1.75 dólares por pie cuadrado. ¿Cuál es el costo total de la aplicación del sellador? (Thomas y Finney, 1996, p. 399.)

INTERPRETACIÓN Y ANÁLISIS DE RESULTADOS
En esta sección presentamos la interpretación y el análisis de las respuestas y actuaciones que exhibieron los estudiantes cuando resolvieron las tareas propuestas.
Para la resolución de las tareas propuestas, los estudiantes utilizaron el pu, el cual tiene como características principales:
• Representación gráfica de las diferentes aproximaciones al área limitada por una función con el eje OX: rectángulos inferiores, rectángulos superiores, punto medio, trapecios y trapecios parabólicos (aproximación de Simpson).
• Aproximaciones numéricas de la integral de una función en un intervalo dado. Las hemos denominado matrices de aproximación y recogen, en la primera columna, el número de subintervalos de integración que se consideran; en la segunda, la aproximación con rectángulos inferiores; en la tercera, con rectángulos punto medio; en la cuarta, con trapecios; en la quinta, con trapecios parabólicos, y en la sexta, con rectángulos superiores.
PROBLEMA 1
En este problema los estudiantes utilizan eficazmente el CAS , mostrando con ello un manejo adecuado de los procedimientos instrumentales. Por ejemplo, Jisbel y Dulce (pareja 3) presentan su solución haciendo uso de las dos representaciones: la gráfica (figura 1) y la numérica. Construyen con el PU la matriz de aproximación (tablas1 y 2).
ECONOMIA
La economía (del griego
οἶκος oikos, ‘casa’, y νόμος nomos, ‘ley’) es la ciencia
social que estudia:
·
La forma o medios de satisfacer las necesidades humanas
mediante los recursos (que se consideran escasos).
·
Con base en los puntos anteriores, la forma en que
individuos y colectividades sobreviven, prosperan y funcionan.
Expresado lo anterior de forma sintética, puede definirse
la economía como la ciencia que estudia «cómo se organiza una sociedad para
producir sus medios de existencia que, distribuidos entre sus miembros y
consumidos por ellos, permiten que la sociedad pueda producirlos de nuevo y así
sucesivamente, proveyendo con ello, de una forma constantemente renovada, la
base material para el conjunto de la reproducción de la sociedad en el tiempo».1
La economía se vale de la psicología y
la filosofía para explicar cómo se
determinan los objetivos; la historia registra
el cambio de objetivos en el tiempo, la sociologíainterpreta el comportamiento humano
en un contexto social y la política explica
las relaciones que intervienen en los procesos económicos.
CALCULO DE AREAS DE FIGURAS PLANAS CON UNA FUNCION
Aplicación de la integral definida
al cálculo de áreas de figuras planas
Área delimitada por una curva y = f(x)
y el eje de abscisas
CASO
I : La función f(x)
es positiva en el intervalo [a, b]
Hallar por integración el área del triángulo formado por la
bisectriz del primer cuadrante al eje OX y
la recta x = 4 . Comparar el resultado con el que se obtiene
geométricamente.


El valor de la integral definida entre los valores
x = 0 y x = 4
es el área encerrada bajo la curva:
CASO
II : La función f(x)
es negativa en el intervalo [a, b]
Hallar el área del recinto limitado por la parábola de la ecuación
y = - x2 , el
eje OX y las rectas x =
2 y x = 4 .


El valor de la integral definida entre los valores
x = 2 y x = 4
es el área encerrada bajo la curva pero cambiada de signo. Es
por esta razón por la que se toma el valor absoluto.
CASO
III : La función f(x)
cambia de signo en el intervalo [a, b]
Hallar por integración el área limitada por el eje OX, la curva
y = x2 - 4 y las
rectas x = 0 y
x = 4 .
En primer lugar calculamos los puntos de corte con el eje OX de la
función:

A continuación estudiamos el signo de la función en cada uno de
los intervalos o se dibuja la gráfica de la función:
|
Intervalo
|
(- ∞, -2)
|
(-2, 2)
|
(2, +∞)
|
|
Punto de prueba
|
f(-3) > 0
|
f(0) < 0
|
f(3) > 0
|
|
Signo de f(x)
|
+
|
-
|
+
|
Como la función entre 0 y 2 es negativa y de 2 a 4 es positiva,
hay un recinto que es negativo (de 0 y 2) y otro positivo (de 2 a 4) :


El área es la suma algebráica de las áreas encerradas por la
gráfica y el eje OX entre los valores
0 y 4 .
Una fórmula es un método práctico de resolver un
asunto, brindar instrucciones o expresar una operación en el ámbito científico.
Uno de los ámbitos más reconocidos para el empleo de
fórmulas es el de la química y la física. Para los científicos químicos, una
fórmula permite resolver operaciones y regular convenciones a la hora de poner
en interacción sustancias y materias.
PROCEDIENTOS
Realizar y llevar a cabo un inventario de todos aquellos procedimientos
que pueden asimilarse como procedimientos contables de acuerdo con la
definición dada al principio, permite conocer en profundidad todas las posibles
operaciones que pueden afectar los estados financieros.
Cuando se está realizando el análisis de todos los procesos llevados a
cabo por la empresa, es sumamente importante determinar e identificar todos
aquellos clasificables como procedimientos contables. Este primer paso del
análisis ayudará a determinar e identificar en cuáles de ellos un error pudiera
tener mayor impacto sobre los estados financieros que otro.
La amortización de una plusvalía por lo general,
representa montos importantes. En una empresa manufacturera, se considera
altamente crítico, el manejo de todos los inventarios, sean éstos de productos terminados, productos en proceso, materias primas o materiales y suministros.
Es probable que para una empresa de servicios el manejo de los inventarios involucre
cifras de poca importancia en comparación a lo que representan éstos para una
empresa
RESULTADOS
Los resultados
pueden ser divididos en varios tipos, dependiendo del procedimiento que se haya
llevado a cabo para obtenerlo. Por ejemplo, en cualquier estudio extensivo un
resultado puede implicar las conclusiones de una investigación, mientras que en algunos juegos o en guerras, el resultado es
la identidad de la facción o equipo perdedor y ganador. En matemáticas, se le
conoce como resultado al valor final de un cálculo, función o expresión estadística.
SUMA DE REIMANN
En matemáticas, la suma de Riemannes un método de
integración numérica que nos sirve para calcular el valor de una integral
definida, es decir, el área bajo una curva, este método es muy útil cuando no
es posible utilizar el Teorema fundamental del cálculo. Estas sumas toman su nombre del matemático alemánBernhard
Riemann.
La suma de Riemann consiste en trazar un número finito de
rectángulos dentro de un área irregular, calcular el área de cada uno de ellos
y sumarlos. El problema de este método de integración numérica es que al sumar
las áreas se obtiene un margen de error muy grande
Teorema fundamental del cálculo
El teorema
fundamental del cálculo consiste (intuitivamente) en la afirmación de
que la derivación e integración de
una función son
operaciones inversas. Esto significa que toda función continua integrable
verifica que la derivada de su integral es igual a ella misma. Este teorema es
central en la rama de las matemáticas denominada análisis matemático o
cálculo.
El teorema es
fundamental porque hasta entonces el cálculo aproximado de áreas -integrales-
en el que se venía trabajando desde Arquímedes,
era una rama de las matemáticas que se seguía por separado al cálculo
diferencial que se venía desarrollando por Isaac
Newton, Isaac
Barrow y Gottfried
Leibniz en el siglo
XVIII y dio lugar a conceptos como el de las derivadas
CALCULO DE
INTEGRALES DEFINIDAS POR METODOS
La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de la suma de infinitos
sumandos, infinitamente pequeños.
El cálculo
integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o anti
derivación, es muy común en la ingeniería y en la ciencia también; se utiliza
principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de
revolución.
Fue usado por primera vez por científicos como Arquímedes, René
Descartes, Isaac
Newton, Gottfried
Leibniz e Isaac
Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo
integral, que propone que la derivación y la integración son procesos
inversos.
CIENCIAS
La ciencia (del latín scientĭa‘conocimiento’) es
el conjunto de conocimientos estructurados sistemáticamente. La ciencia es el
conocimiento obtenido mediante la observación de patrones regulares, de
razonamientos y de experimentación en ámbitos específicos, a partir de los
cuales se generan preguntas, se construyen hipótesis, se
deducen principios y se elaboran leyes
La ciencia considera distintos hechos, que deben ser objetivos y observables. Estos
hechos observados se organizan por medio de diferentes métodos y técnicas,
(modelos y teorías) con el fin de generar nuevos conocimientos.
INGENIERIA
La ingeniería es el conjunto de conocimientos y
técnicas científicas aplicadas al desarrollo, implementación, mantenimiento y
perfeccionamiento de estructuras (tanto físicas como teóricas) para la
resolución de problemas que afectan la actividad cotidiana de la sociedad.
Para ella, el estudio, conocimiento, manejo y dominio de las matemáticas, la
física y otras ciencias es aplicado profesionalmente tanto para el
desarrollo de tecnologías, como para el manejo eficiente de recursos y/o
fuerzas de la naturaleza en beneficio de la sociedad. La ingeniería es la
actividad de transformar el conocimiento en algo práctico.
Otra característica que define a la ingeniería es la aplicación
de los conocimientos científicos a la invención o perfeccionamiento de nuevas
técnicas.
ADMINISTRACION
La administración como
una ciencia social compuesta de principios, técnicas y prácticas y cuya
aplicación a conjuntos humanos permite establecer sistemas racionales de
esfuerzo cooperativo, a través de los cuales se puede alcanzar propósitos
comunes que individualmente no es factible lograr.
































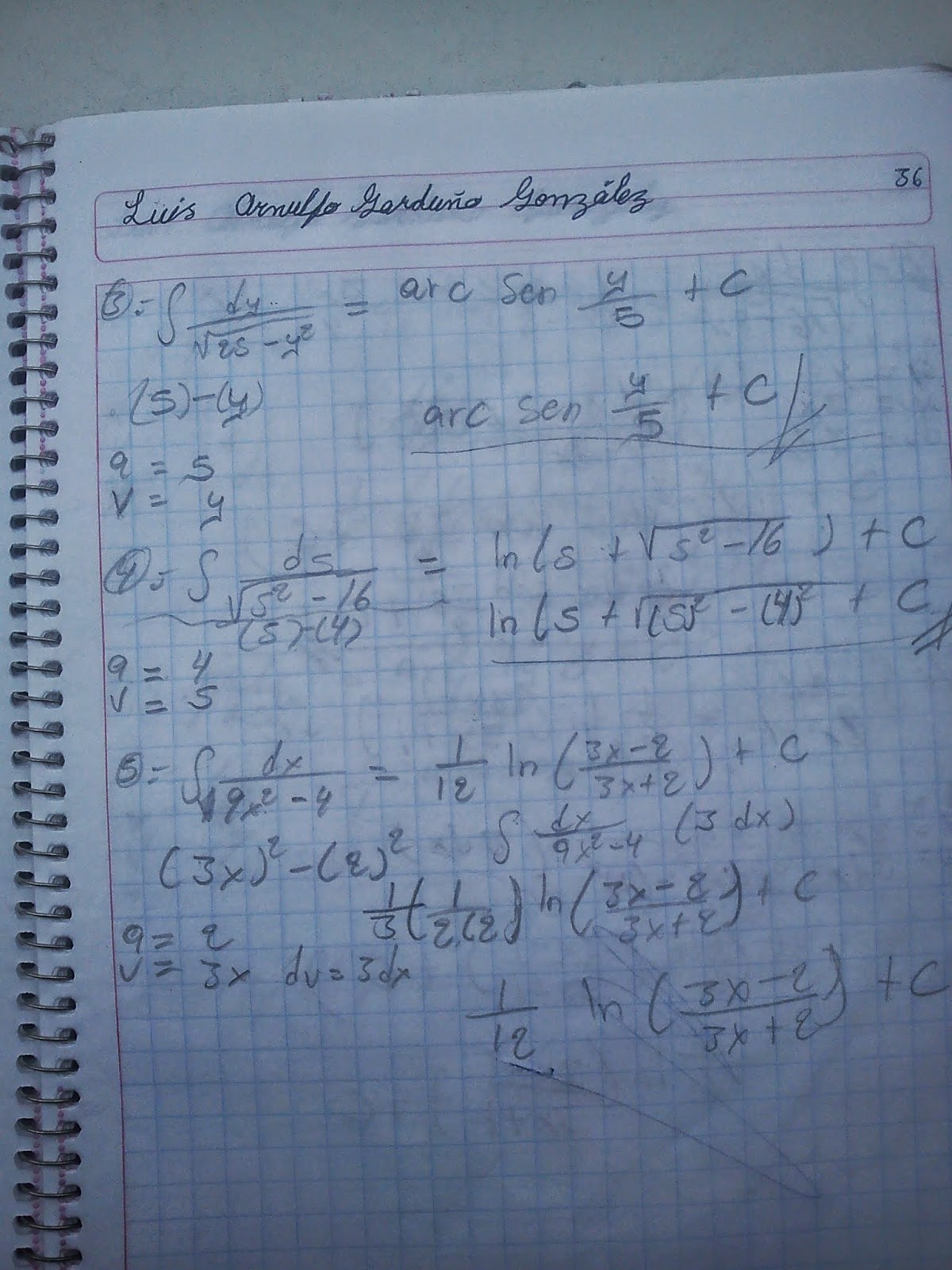

















Debe de llevar portada, foto de los integrantes del equipo, programa, información en cada tema, los ejercicios escaneados o en foto, los videos resolviendo un ejercicio cada integrante del equipo y hacer comentarios a los demás equipos en su blog.
ResponderBorrarDarle una mejor presentación y cambiar los colores de fondo
ResponderBorrarMuy bin compañeros una sugerencia seria que cambiaran el color del fondo para que se vea mas presentable.
ResponderBorrarvan bien solo una observación la imagen no se alcanza a distinguir háganla un poco mas grande y suban un poco mas de información y todo esta perfecto
ResponderBorrarola pues les falta mas información la foto grupal y sin ofender cambien el color de fondo que si lastima para leer pero van bien
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarJose Antonio Vanegas Martinez .Compañeros le falta mas presentación a su blog ademas de mucha información xfavor cambien el color del fondo
BorrarVioleta Garduño Zepeda
ResponderBorrartodo bien compañeros hay la llevan suerte
Javier Armando Sarabia García
ResponderBorrarel diseño esta bien pero falta información suerte ustedes pueden
bien compañeros les falta los videos y les falta un poco mas de temario pero todo vien aqui les dejo el mio el link
ResponderBorrarhttp://info6206.blogspot.mx/search/label/inicio
Luisa Angela Garcia Lopez
ResponderBorrarvan muy bien chicos suerte les falta información pero van bien
daniel leon cuevas van bien compañeros pero les falta informacin y los videos
ResponderBorrarJose Antonio Vanegas Martinez. Compañeros les falto demasiada pero demasiada información,ademas el texto se pierde con el fondo y la letra es muy pequeña
ResponderBorrarSalvador Mariano Segundo. Les hace falta demasiada información
ResponderBorrarNanci Karina Perez Salgado
ResponderBorrarmuy bien chicos
blanca edith sanchez dominguez. compañeros las imagenes de la libreta no se pueden distinguir los ejercicios y les falto mas informacion
ResponderBorrarMARIA HORTENSIA MUNGUIA ROMERO
ResponderBorrarVAN BIEN COMPAÑEROS
DIANA LAURA PIÑA CRUZ
MUY BIEN PERO LES FALTAN LOS VIDEOS
JOSELYNE ESQUIVEL CARMONA
VAN BIEN NADA MAS QUE ALGUNAS IMAGENES NO SE VEN
Este comentario ha sido eliminado por el autor.
ResponderBorrarGERARDO PANIAGUA SANCHEZ
ResponderBorrarbien compañeros nadamas que hay una parte donde no se distinguen las letras
JOSE ISRAEL HERNANDEZ PARADA
todo bien compañeros solo que las imagenes no se pueden ver
JORGE BULMARO PANIAGUA SANCHEZ
va bien compañeros solo que les faltan los videos
Y los videos donde están, falta un integrante del equipo en la foto y con uniforme completo no con el pans
ResponderBorrar